1. Introducción
La formación en matemáticas es fundamental porque el conocimiento matemático contribuye con el progreso de las sociedades en los aspectos científico, tecnológico y económico, entre otras áreas del conocimiento humano (Camero et al., 2016). Para lograr una buena preparación en esta disciplina se requiere un alfabetismo funcional (Skovsmose & Valero, 2013), el cual puede estar orientado por un profesor de matemáticas que, a través de la reflexión constante de su práctica, esté en continua mejora y adaptación de acuerdo con las circunstancias actuales y requerimientos de la sociedad.
Las investigaciones de los últimos años han reportado que los conocimientos y las creencias que tiene el profesor sobre las matemáticas, su enseñanza y su aprendizaje están altamente vinculados con su quehacer en el aula (Ernest, 1989; Furinghetti & Morselli, 2011; Pajares, 1992; Schoenfeld, 1998; Siswono et al., 2019). Raymond (1997) ha evidenciado la falta de coherencia que tienen los maestros sobre estas tres creencias, puesto que no se reflejan en su práctica de enseñanza. Otros estudios han demostrado que las creencias de los profesores pueden influir positivamente sobre el rendimiento de los estudiantes, si estas tienden a posturas constructivistas (Bermejo et al., 2021; Vintere, 2018).
El hecho de identificar las creencias que tienen los profesores sobre las matemáticas, cómo las enseñan y cómo conciben el aprendizaje de la disciplina permite influir sobre ellas para fortalecerlas o transformarlas con el fin de mejorar los procesos de enseñanza-aprendizaje en las aulas (Koklu & Phan, 2020; Thurm & Barzel, 2020), es decir, su práctica de la enseñanza (Ernest, 1989), y posiblemente el rendimiento de sus estudiantes (Muhtarom et al., 2018).
Sin embargo, son pocos los estudios sobre las creencias de los profesores de secundaria de matemáticas en servicio (Beswick, 2012; Kardanova et al., 2014; Purmono, 2017; Xie & Cai, 2021), lo que complejiza su conocimiento y la posibilidad de realizar programas de formación docente acorde con las necesidades reales (Purmono, 2017), y desperdicia la oportunidad de mejorarlas y reconstruir la práctica para que exista coherencia entre estas (Calleja, 2022). Por tanto, en este estudio se considera importante identificar las creencias de los profesores de matemáticas de secundaria en ejercicio a través de un instrumento que las evalúe en relación con la disciplina propia, su enseñanza y su aprendizaje, y determinar la correlación entre estas tres variables y el perfil de los profesores.
2. Creencias sobre las matemáticas, su enseñanza y su aprendizaje
En esta investigación las creencias se conciben como reglas, conceptos explícitos o implícitos (Wang & Cai, 2007) que orientan e inciden en el quehacer del aula (Beswick, 2012), y su estudio es de gran importancia debido a su relación con la práctica (Ernest, 1989).
Actualmente existen diversas posturas teóricas respecto a las creencias sobre las matemáticas, su enseñanza y su aprendizaje. Están las filosóficas como las absolutistas y las mecanicistas, que entienden las matemáticas como una ciencia exacta, con verdades universales (Dayal & Lingam, 2020), y las falibilistas y realistas, en las que las matemáticas son una creación humana, un producto cultural que evoluciona (Corkin et al., 2015). Aquellas creencias con una mirada pedagógica son las trasmisionistas y constructivistas, que se enfocan únicamente en la enseñanza y el aprendizaje de las matemáticas (Clark et al., 2014; Goos et al., 2021; Guangbao & Timothy, 2021). Las trasmisionistas dan relevancia a la transferencia de conocimientos que tiene el profesor, y el estudiante es un receptor pasivo que repite. Las constructivistas conciben que el educando es el centro del proceso de enseñanza aprendizaje, es él quien construye, conjetura y crea, y el profesor cumple el rol de orientador.
Por último, están las creencias tripartitas, que manejan una postura intermedia entre dos extremos. Entre estas se destacan tres perspectivas teóricas: a) instrumentalistas, platonistas y resolución de problemas (Ernest, 1989); b) transmisión, descubrimiento y conexión (Askew et al., 1997), y c) formalistas, caja de herramientas y proceso (asociadas a una visión estructurada del mundo) (Grigutsch et al., 1998). En un extremo se encuentran las instrumentalistas, trasmisionistas y formalistas; en estas posturas se entienden las matemáticas como un conjunto de múltiples reglas, hechos estáticos y verdades universales. En la posición intermedia se encuentran las platonistas, de descubrimiento y caja de herramientas, en las que la disciplina es estática y está organizada a través de verdades lógicas, conceptos, habilidades y procedimientos. En el otro extremo se ubican las de resolución de problemas, conexión y proceso; bajo esta mirada las matemáticas son una disciplina que evoluciona, es dinámica, genera conjeturas e interacción con diferentes conocimientos.
En relación con las creencias sobre la enseñanza y el aprendizaje, las posturas extremas (instrumentalistas, trasmisionistas y formalistas) asumen visiones similares a las tradicionales, y en el otro extremo (resolución de problemas, descubrimiento y proceso) a posturas constructivistas. Se podría decir que, de acuerdo con las necesidades actuales de formación matemática, las creencias menos adecuadas en los profesores de matemáticas de secundaria corresponden a aquellas en que las matemáticas son un ente estático, el estudiante es un receptor y el profesor es la fuente del conocimiento. Las más adecuadas consideran las matemáticas como una creación del cerebro humano; por tanto, evolucionan, el estudiante es un sujeto activo y el profesor es un guía. Las creencias que se ubican en el medio han sido consideradas en esta investigación como ligeramente adecuadas porque en ocasiones se transita por estas para llegar a las que se espera (Swan & Swain, 2010; Vale et al., 2020), es decir, a las asociadas a la resolución de problemas.
Las creencias que se evaluaron en este trabajo corresponden a las definidas por Ernest (1989), puesto que es uno de los pioneros en este tema y en manifestar la relación que tienen con la práctica de la enseñanza. Además, la literatura internacional reporta varias investigaciones en profesores de secundaria apoyadas en esta perspectiva teórica que promueve la relación de las tres variables con la práctica (Misfeldt et al., 2016; Muhtarom et al., 2018; Safrudiannur & Rott, 2021; Vale et al., 2020; 2021). En la Tabla 1 se observa de manera detallada la visión de cada creencia con respecto a la visión generada por Ernest (1989); también se puede establecer una similitud con las expuestas anteriormente.
Tabla 1. Creencias sobre las matemáticas, su enseñanza y su aprendizaje según Ernest (1989)
Creencias | Matemáticas | Enseñanza | Aprendizaje |
Instrumentalistas | Conjunto de reglas, hechos inamovibles y estáticos. Procedimientos estándar y verdades universales. Exactitud y precisión en la disciplina. | Procedimientos matemáticos. Transferencia directa de conocimientos. Modelo de enseñanza del instructor. | Refuerzo de algoritmos. Aprendizaje jerárquico. Estudiante pasivo. Actividad individual basada en observar, escuchar e imitar. |
Platonistas | Verdades lógicas. Contenidos organizados. Es estática. Estructurada por reglas, habilidades y procedimientos. | Modelo explicativo. Se centra en la comprensión de temas. Definiciones y demostraciones. Fórmulas y algoritmos, que se mecanizan y aplican en ejercicios rutinarios. | Comprensión de conceptos y procedimientos a través de ejemplos para que el estudiante siempre pueda resolver problemas. Privilegia la actividad individual de los estudiantes. |
Resolución de problemas | Construida por la mente humana, evolutiva. | Desarrollo de razonamiento y habilidades matemáticas. Trabajo grupal e interacción con el profesor. Enseñanza basada en preguntas y solución de problemas. | Estudiante autónomo, explora, debate, propone y crea estrategias de solución de problemas. Promueve el ejercicio interactivo, el debate y la creatividad para la solución de ejercicios no rutinarios. |
Nota. Fuente: Ernest (1989).
2.1. Relación entre las creencias de las matemáticas, su enseñanza y su aprendizaje
Algunos autores han mencionado la relevancia que tienen las creencias sobre las matemáticas, su enseñanza y su aprendizaje en los profesores de matemáticas de secundaria para alcanzar o no el éxito de las reformas curriculares actuales de esta disciplina (Askew & William, 1997; Pajares, 1992; Thompson, 1992). No existe un consenso si hay relación entre estas tres variables o no. Vale et al.(2021) mencionan que es complejo encontrar una relación de coherencia entre estas tres variables debido a que el avance o la progresión en ellas están ligadas a la experiencia y formación profesional. Además, puede suceder que los sistemas de creencias no se encuentren organizados de forma lógica (Xenofontos, 2018). Por otra parte, Safrudiannur y Rott (2021) afirman que las creencias que los profesores manifiesten dependen del tipo de estudiantes con los que realicen su práctica de enseñanza; es decir, si sus aprendices están entrenados en la solución de problemas matemáticos, el profesor tendrá creencias más deseables. Asimismo, Mutharom et al.(2018) encontraron que existe una relación entre las creencias de los maestros y de los estudiantes, específicamente frente a la mirada platonista.
Purmono (2017) menciona que existe una conexión entre las creencias sobre el aprendizaje y la enseñanza de las matemáticas, la razón obedece a que los profesores tienen por objetivo que sus estudiantes aprendan lo mejor posible. En su estudio, Dayal et al.(2019) muestran que es más probable que haya una fuerte coherencia entre las creencias de la enseñanza y el aprendizaje de las matemáticas que en relación con la disciplina, y alude que tanto la experiencia personal como profesional alimentan las primeras dos, mientras que las matemáticas se aprenden formalmente en una institución educativa.
Asimismo, Misfeldt et al.(2016) plantean que si un profesor tiene creencias instrumentalistas, tendrá una tendencia a creer que en él debe estar centrado el proceso de enseñanza-aprendizaje; de ahí que el aprendizaje debe focalizarse en la repetición de procedimientos. También se han establecido relaciones con respecto al clima en el aula: el estudio de Guangbao y Timothy (2021) encontró que si las creencias son positivas o adecuadas, la actitud en el aula es favorable para el aprendizaje de las matemáticas.
Existen otras posturas sobre la relación y la progresión de las creencias. Swan y Swain (2010) consideran que las creencias pueden evolucionar de un lugar a otro: pasar de una creencia menos adecuada a una ligeramente adecuada (transmisionismo a conexionismo), de una ligeramente adecuada a una más adecuada (conexionismo a descubrimiento), o dar el salto extremo (transmisionismo a descubrimiento). Esta misma situación mencionan Xie y Cai (2021) al expresar que los profesores pueden transitar de posturas constructivistas a tradicionales a lo largo de los años, lo que evidencia que no hay estabilidad en ninguna de las dos posturas. Una situación similar presentan Furinghetti y Morselli (2011), quienes demostraron que a través de la formación docente, los profesores transitaron de visiones platonistas a de resolución de problemas.
Por otra parte, Beswick (2012) menciona que las creencias que se tienen sobre las matemáticas influyen sobre cómo se deben enseñar. Además, menciona que la coherencia entre las matemáticas, su enseñanza y su aprendizaje es posible si están fuertemente ligadas a un contexto particular (Beswick, 2005). Es decir, que los profesores que se encuentran en un contexto parecido tienden a tener una creencia parecida a la cultura en la cual están inmersos (Siswono et al., 2019; Xenofontos, 2018).
Este panorama invita a los investigadores en educación matemática a seguir estudiando las creencias de los profesores de matemáticas de secundaria porque, si bien no se ha generalizado su relación con la práctica de la enseñanza, se tiene certeza de que inciden en el comportamiento y en el porqué de las acciones que realizan en el aula (Šunderlík & Rybanský, 2015), así como en el desempeño académico de los estudiantes (Muhtarom et al., 2018). Además, existe el interés a nivel internacional de que las reformas curriculares para la enseñanza de las matemáticas estén centradas en el estudiante (Ministerio de Educación Nacional, 1998; National Council of Teachers of Mathematics, 2015; Šunderlík & Rybanský, 2015). Por tanto, es importante identificar las creencias de los profesores y cómo cambian para transformarlas a través de programas de desarrollo profesional que tomen en cuenta el aprendizaje de los estudiantes (Philipp, 2007; Vesga & Ángel, 2021).
3. Método
3.1. Procedimiento
Para identificar las creencias sobre las matemáticas, su enseñanza y su aprendizaje, así como la correlación entre estas tres variables, y determinar el perfil de los profesores de matemáticas de secundaria, se administró un cuestionario en el primer semestre de 2023, en formato online a través de Google Forms, después de la firma del consentimiento informado por parte de los profesores participantes. Luego se recolectaron los datos de forma sincrónica y se hizo el respectivo análisis. La población de este estudio corresponde a una muestra compuesta por docentes de matemáticas de secundaria, en servicio, de Colombia.
3.2. Análisis de los datos
El enfoque de esta investigación es cuantitativo, a través de un muestreo no probabilístico por conveniencia (Creswell, 2012; Hernández Sampieri et al., 2014), lo cual permitió cumplir con el objetivo propuesto. Se usó el software SPSS versión 25 para el análisis de los datos. Se utilizó estadística descriptiva para identificar las creencias de los profesores, la prueba de chi-cuadrado para establecer la correlación entre las variables, y la fórmula de Siswono et al.(2016) y Siswono et al.(2019) para establecer los perfiles. Los resultados se presentan en tres apartados: puntuaciones absolutas obtenidas por los profesores, correlaciones entre las variables evaluadas y perfiles del profesorado.
3.3. Instrumento
En este estudio se usó el Cuestionario de Opciones Múltiples sobre las Creencias de las Matemáticas, su Enseñanza y Aprendizaje (COMEA), el cual fue diseñado para identificar las creencias de los profesores de secundaria de matemáticas asociadas a estas tres variables e identificar un perfil con base en la teoría de Ernest (1989). Para su diseño se usaron los trabajos realizados por Safrudiannur y Rott (2021) y Siswono et al. (2016) y Siswono et al. (2019), quienes habían estudiado dichas creencias desde la perspectiva de Ernest (1989), pero asociadas exclusivamente a la resolución de problemas (para más detalles sobre el diseño y la validación del instrumento, ver Ángel et al. (2024)). El cuestionario reporta un alfa de Cronbach global de .803, valor que garantiza una consistencia interna buena, y un KMO de .767. Además, el análisis factorial confirmatorio muestra un chi-cuadrado de 2.975, lo que indica un ajuste perfecto; un RMSEA de .051 aceptable, el CFI de .715 que muestra un ajuste adecuado, y un SRMR de .075 que indica que el cuestionario permite evaluar las creencias de los profesores.
El instrumento está compuesto por 33 ítems divididos en tres partes iguales. Los primeros 11 corresponden a creencias sobre las matemáticas, los siguientes 11 a creencias sobre la enseñanza de las matemáticas, y los últimos 11 a creencias sobre el aprendizaje de las matemáticas. Cada ítem presenta tres opciones de respuesta: la instrumentalista, la platonista y la de resolución de problemas. La opción deseable o correcta es la asociada con las creencias de resolución de problemas, mientras que la instrumentalista y la platonista se consideran incorrectas.
Para determinar el perfil de creencias de los profesores de cada uno de los ítems se usó la fórmula de Siswono et al. (2016) y Siswono et al. (2019) que se presenta a continuación,

y la interpretación de los resultados se muestra en la Tabla 2. Se puntuó cada opción de respuesta de los participantes de la siguiente manera: 1.00 instrumentalista, 2.00 platonista, y 3.00 resolución de problemas.
Tabla 2. Perfil del profesorado de acuerdo con Siswono et al. (2016; 2019)
Puntuación (S) | Nivel de creencias |
1.00 ≤ S ≤ 1.67 | instrumentalista |
1.67 < S ≤ 2.33 | platonista |
2.33 < S ≤ 3.00 | resolución de problemas |
Nota. Formula tomada de Siswono et al. (2016) y Siswono et al. (2019).
3.4. Participantes
El estudio se realizó con 199 profesores de matemáticas de secundaria y media de Colombia. Todos se encontraban ejerciendo la enseñanza de las matemáticas en colegios oficiales o privados del país durante el primer semestre de 2023. Las materias que impartían eran Cálculo, Trigonometría, Álgebra, Aritmética, Geometría y Estadística.
La muestra estaba conformada por 102 mujeres (51.3 %) y 97 hombres (48.7 %). Respecto a la edad, 9 (4.5 %) se encuentran en un rango menor a 25 años; 61 (30.7 %) entre 25 y 35; 70 (35.2 %) entre 36 y 45; 41 (20.6 %) entre 46 y 55; y 18 (9 %) más de 55 años. Con relación a la experiencia profesional, 28 han laborado menos de 5 años (14.0 %); 46 entre 5 y 10 años (23.1 %); 35 de 11 a 15 años (17.6 %), 36 en el intervalo de 16 a 20 años (18.1 %); 33 con 21 a 25 años (16.6 %); y 21 más de 26 años (10.6 %).
La formación profesional que han recibido los participantes en pregrado es diversa, puesto que algunos han sido formados como licenciados en matemáticas o afines a esta disciplina, et al. son profesionales de otras áreas. En Colombia, a partir del Decreto 1278 (2002) se reglamentó que cualquier profesional que conozca una disciplina puede enseñarla en una institución educativa escolar, siempre y cuando haya realizado algún curso de pedagogía o relacionado con esta. En la Figura 1 se presenta la preparación en cuanto a pregrado y posgrado.
Figura 1. Formación profesional de los profesores del estudio
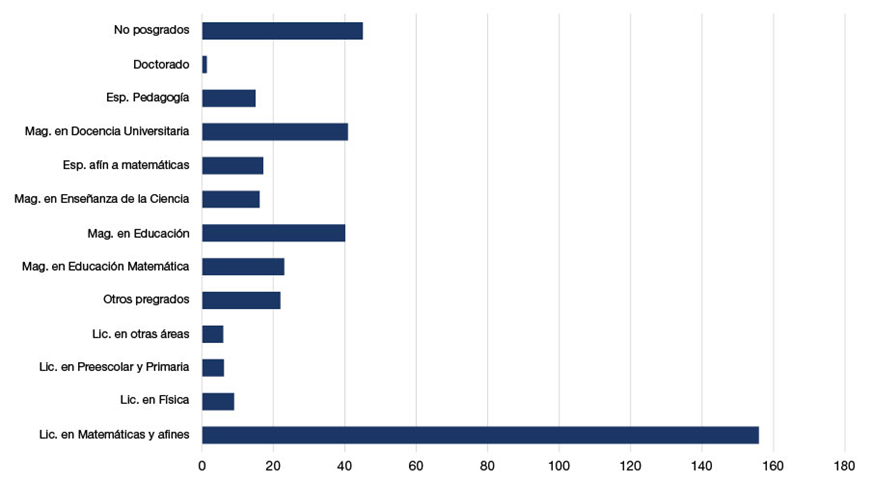
Nota. Caracterización Google Forms.
Como se observa en la Figura 1, la mayoría de los profesores tienen una preparación de licenciado en Matemáticas, en Educación Básica Orientada a las Matemáticas o Matemáticas y Física (78.4 %), y los demás (21.6 %) están formados como licenciados en Educación Primaria, Preescolar, Química, Física o carreras profesionales como Contaduría, Química pura e ingenierías. En relación con la formación posgradual, se observa que solo el 22.6 % no ha realizado ninguna. Las maestrías más cursadas con porcentajes similares son las de Docencia Universitaria (20.6 %) y de Educación (20.1 %). Además, solo un participante tiene formación de doctor.
4. Resultados
4.1. Puntuaciones absolutas obtenidas por los profesores participantes
En este apartado se presentan los resultados que corresponden al puntaje total obtenido en cada uno de los ítems de las tres variables evaluadas. Cada respuesta se puntuó con 1 si era correcta y con 0 si no lo era. Estas puntuaciones permitieron identificar las creencias de los profesores participantes.
En la Tabla 3 se observa que en las tres variables evaluadas se alcanzó a 11 el mayor número de ítems correctos, lo que equivale al total de ítems. En las creencias sobre las matemáticas y sobre la enseñanza de las matemáticas, el puntaje más bajo obtenido por los participantes fue 2, y en las creencias sobre el aprendizaje de las matemáticas fue 0. Los puntajes más frecuentes para las creencias sobre las matemáticas fueron 6 y 7, en creencias sobre la enseñanza, 8, y sobre el aprendizaje, 8. Se observa que el total de aciertos en cada variable fue de 199.
Tabla 3. Número de aciertos por variable e ítem de los profesores (n = 199)
Aciertos | Creencias sobre las matemáticas | Creencias sobre la enseñanza de matemáticas | Creencias sobre el aprendizaje de matemáticas |
0 | 0 | 0 | 1 |
1 | 0 | 0 | 6 |
2 | 3 | 6 | 4 |
3 | 17 | 12 | 9 |
4 | 19 | 11 | 12 |
5 | 31 | 17 | 16 |
6 | 39 | 31 | 30 |
7 | 39 | 26 | 31 |
8 | 20 | 37 | 37 |
9 | 12 | 23 | 30 |
10 | 15 | 27 | 19 |
11 | 4 | 9 | 4 |
Nota. Respuestas correctas para las creencias en Google Forms.
En la Tabla 4 se presentan la media y la desviación estándar del número de ítems que respondieron correctamente los 199 profesores participantes. Se observa que los resultados obtenidos en las creencias sobre la enseñanza de las matemáticas son ligeramente mayores que en las otras dos variables. Todos los valores medios están por encima de la mitad del número de ítems. Se podría decir en general que en las tres variables las creencias de los profesores participantes son probablemente adecuadas.
Tabla 4. Promedio del número de ítems correctos
Variables | Creencias sobre las matemáticas | Creencias sobre la enseñanza de matemáticas | Creencias sobre el aprendizaje de matemáticas |
6.31 | 7.12 | 6.86 | |
6 | 7 | 7 | |
2.07 | 2.30 | 2.35 |
Nota. Los estadísticos descriptivos se calcularon con SPSS.
4.2. Correlaciones entre las variables categóricas evaluadas
Para determinar si existe correlación entre las variables estudiadas se realizó la prueba de independencia chi-cuadrado. Esta prueba permitió determinar si las variables cualitativas estaban asociadas, es decir, si una depende de otra. Las variables evaluadas por el instrumento son las creencias asociadas a las matemáticas, su enseñanza y su aprendizaje. El nivel de error con el que se trabajó corresponde al .005, de manera que si el valor de significancia sobrepasa este nivel no existe relación entre las variables. En cuanto a la medida de dependencia se revisó el coeficiente de contingencia, el cual tiene un rango de 0 a 1, cuanto más se acerca a 1, más grande es la dependencia entre las variables. Para calcular la intensidad o fuerza entre dos variables se usó la V de Cramer —puesto que estamos comparando más de cinco filas y columnas por cada variable—, que toma valores entre 0 y 1: si el resultado es mayor que 0 y menor que .2 no hay asociación; igual a .2, la asociación es débil; mayor que .2 y menor que .6, la asociación es moderada; y mayor que .6, la relación es fuerte.
En la Tabla 5 se muestra el resultado de chi-cuadrado con un nivel de significancia de .001; contrastado con el nivel de error establecido, permite inferir que hay una relación significativa entre las puntuaciones totales de las creencias asociadas a las matemáticas y las asociadas a la enseñanza de las matemáticas. Se obtuvo un V de Cramer de .261, lo cual implica que la asociación es moderada.
Tabla 5. Relación entre las creencias asociadas a las matemáticas y las asociadas a la enseñanza de las matemáticas
Prueba chi-cuadrado | |||
valor | df | Significación asintótica bilateral | |
Chi-cuadrado de Pearson | 121.562 | 81 | 0.002 |
Razón de verosimilitudes | 114.696 | 81 | 0.008 |
V de Cramer | 0.261 | 0.002 | |
Número de casos validos | 199 | ||
Nota. Se calculó chi cuadrado con p < 0.05.
En la Tabla 6 se observa que el nivel de significancia obtenido también fue de .001, de lo que se infiere que entre las creencias asociadas a las matemáticas y las asociadas al aprendizaje de las matemáticas hay una relación significativa. También se corrobora que la asociación es moderada entre estas dos variables, puesto que el valor de V de Cramer obtenido fue de .286.
Tabla 6. Relación entre las creencias asociadas a las matemáticas y las asociadas al aprendizaje de las matemáticas
Prueba chi-cuadrado | |||
Valor | df | Significación asintótica bilateral | |
Chi-cuadrado de Pearson | 146.568 | 99 | 0.001 |
Razón de verosimilitudes | 118.508 | 99 | 0.088 |
V de Cramer | 0.286 | 0.001 | |
Número de casos validos | 199 | ||
Nota. Se calculó chi cuadrado con p < 0.05.
En relación con la asociación entre las puntuaciones totales de las creencias sobre la enseñanza de las matemáticas y sobre su aprendizaje, se observa en la Tabla 7 que el nivel de significancia obtenido también fue de .000, lo que implica que existe una relación significativa entre estas dos variables. La relación es moderada, un V de Cramer de .360, el cual es más alto que las otras dos comparaciones realizadas.
Tabla 7. Relación entre las creencias asociadas a la enseñanza de las matemáticas y las asociadas a su aprendizaje
Prueba chi-cuadrado | |||
valor | df | Significación asintótica bilateral | |
Chi-cuadrado de Pearson | 232.678 | 99 | 0.000 |
Razón de verosimilitudes | 188.451 | 99 | 0.000 |
V de Cramer | 0.360 | 0.000 | |
Número de casos validos | 199 | ||
Nota. Se calculó chi cuadrado con p < 0.05.
4.3. Perfil de las creencias de los profesores
Por último, para determinar los perfiles obtenidos por los participantes se implementó la fórmula de Siswono et al. (2016) y Siswono et al. (2019), en la que se puntuó las creencias I con 1, las P con 2 y las de RP con 3. En la Tabla 8 se encuentran los ítems del bloque del instrumento que se refiere a creencias sobre las matemáticas, las de la columna RP se refieren a la visión de la Resolución de Problemas — se consideran aciertos en esta investigación—, las de la P corresponden a las platonistas, y las de la I a las instrumentalistas. Aplicando la fórmula mencionada se encontró que, de los 199 participantes de este estudio, el 68.84 % (137) tiende a un perfil de RP, el 30.65 % (61) a un perfil P, y el porcentaje restante a I.
Tabla 8. Respuestas asociada a las creencias sobre las matemáticas
Ítem | RP | P | I |
1 | 59 | 78 | 62 |
2 | 114 | 59 | 26 |
3 | 145 | 18 | 36 |
4 | 133 | 39 | 27 |
5 | 182 | 14 | 3 |
6 | 137 | 22 | 40 |
7 | 32 | 71 | 96 |
8 | 60 | 96 | 43 |
9 | 122 | 57 | 20 |
10 | 127 | 34 | 38 |
11 | 126 | 35 | 38 |
Nota. Frecuencia obtenida por los participantes en el tipo de creencia.
En la Tabla 9 se presentan los resultados del segundo bloque de preguntas, en el que el 65.82 % (131) tiene una visión de creencia sobre la enseñanza de las matemáticas asociada a la RP y el 34.17 % (68) a la P. En esta variable no se encontró ningún profesor con una visión I de la enseñanza de las matemáticas.
Tabla 9. Respuestas asociadas a las creencias sobre la enseñanza de las matemáticas
Ítem | RP | P | I |
12 | 123 | 28 | 48 |
13 | 179 | 15 | 5 |
14 | 55 | 65 | 79 |
15 | 131 | 34 | 34 |
16 | 110 | 83 | 6 |
17 | 136 | 25 | 38 |
18 | 141 | 52 | 6 |
19 | 42 | 157 | 0 |
20 | 148 | 32 | 19 |
21 | 192 | 0 | 7 |
22 | 161 | 31 | 7 |
Nota. Frecuencia obtenida por los participantes en el tipo de creencia.
En el perfil de las creencias sobre la enseñanza de las matemáticas tampoco se encuentran profesores con una visión I. En la Tabla 10 se encuentran las respuestas y se observa que el 81.9 % (163) presenta un perfil RP y el 18.1 % restante corresponde a la visión P.
Tabla 10. Respuestas asociadas a las creencias sobre la enseñanza de las matemáticas
Ítem | RP | P | I |
23 | 162 | 31 | 6 |
24 | 150 | 26 | 23 |
25 | 167 | 21 | 11 |
26 | 82 | 114 | 3 |
27 | 131 | 52 | 16 |
28 | 123 | 65 | 11 |
29 | 47 | 148 | 4 |
30 | 53 | 130 | 16 |
31 | 146 | 44 | 9 |
32 | 169 | 22 | 8 |
33 | 122 | 67 | 10 |
Nota. Frecuencia obtenida por los participantes en el tipo de creencia.
5. Discusión y conclusiones
Se identificó que las creencias sobre las matemáticas, su enseñanza y su aprendizaje en los 199 profesores de matemáticas de secundaria en servicio se encuentran por encima de la mitad (5.5) del total de los ítems de cada variable en las puntuaciones absolutas del instrumento, hecho que indica que las creencias están entre aquellas que se consideran medianamente adecuadas (platonistas) y adecuadas (resolución de problemas). Esto se corroboró al calcular las medias y medianas de cada variable y se obtuvieron valores iguales o superiores a 6. Los resultados revelan que los profesores de la muestra tienden a tener creencias más cercanas a las visiones platonistas y de resolución de problemas.
En cuanto a la relación de dependencia entre las tres variables estudiadas, se confirma su asociación a través de la prueba de independencia de chi-cuadrado al obtener un valor de significancia menor que .005 y un coeficiente de contingencia que tiende a 1 en cada par de variables. En consecuencia, existe dependencia entre las creencias sobre las matemáticas, su enseñanza y su aprendizaje. Este hallazgo se puede deber al hecho de que todos los profesores evaluados pertenecen al mismo contexto cultural (Beswick, 2005; Siswono et al., 2019; Xenofontos, 2018).
Estas conclusiones se confirman por medio del valor obtenido en el estadístico V de Cramer que, al ser superior a .2, determina que existe una relación moderada entre las creencias sobre las matemáticas y las creencias sobre la enseñanza de las matemáticas, lo cual coincide con lo reportado por Beswick (2012), quien afirmó que las primeras inciden en la forma de concebir el proceso de enseñanza, las creencias sobre las matemáticas y las creencias sobre el aprendizaje de las matemáticas, y las creencias sobre la enseñanza y el aprendizaje de las matemáticas; esta última presenta una relación más intensa que las otras dos, puesto que tuvo un valor ligeramente más alto. Los resultados van en la misma línea de Purmono (2017) y de Dayal et al. (2019), que reportan que la relación más fuerte se da entre los procesos de enseñanza-aprendizaje, y están en oposición a Vale et al. (2021), porque a través del instrumento fue posible encontrar la coherencia entre las tres variables.
En cuanto a los perfiles que presentaron los 199 profesores de la muestra a través de la fórmula de Siswono et al. (2016) y Siswono et al. (2019), se observa que el mayor porcentaje declara tener creencias en las tres variables asociadas a la visión de resolución de problemas, seguido por las platonistas y, en un porcentaje menor, las instrumentalistas. Este resultado aporta conocimientos para realizar programas de formación docente encaminados a fortalecer las creencias de los profesores de matemáticas de secundaria y hacerlas progresar hacia las más adecuadas, que, de acuerdo con este estudio, son las de resolución de problemas (Furinghetti, & Morselli, 2011; Swan y Swain, 2010; Xie y Cai, 2021). Esto va de la mano con los documentos orientadores del Ministerio de Educación Nacional (1998, 2006), que propende al desarrollo de procesos de enseñanza-aprendizaje de las matemáticas a través de aprendizajes significativos en los que el estudiante sea el centro del proceso y en donde las matemáticas se conciban como una construcción cultural. De manera que, de acuerdo con la UNESCO (2015), se puedan realizar prácticas de enseñanza que se relacionen positivamente con el aprendizaje, para así alcanzar mayores niveles de desempeño.
Cabe resaltar que los resultados de este estudio responden a las puntuaciones dadas por las respuestas seleccionadas por los profesores en el cuestionario COMEA, hecho que puede ser un factor limitante en cuanto a la identificación y el perfil de las creencias. Sería pertinente, en investigaciones futuras, corroborar estos hallazgos con la observación de la práctica de la enseñanza, entrevistas u otros instrumentos, que permitan establecer la coherencia entre lo que declaran y lo que hacen los profesores. Además, sería interesante que el instrumento se aplicara en otros países de América Latina y se hicieran comparaciones para establecer las creencias que predominan en los docentes y reflexionar sobre los resultados del aprendizaje de los estudiantes.
Agradecimientos y reconocimientos
Esta investigación fue posible gracias al apoyo de la Secretaría de Educación del Distrito de Bogotá, que concedió un permiso de estudios a la investigadora principal.
Referencias bibliográficas
Angel-Cuervo, Z. M., Briceño-Martínez, J. J., & Bernal-Ballén, A. (2024). Validation of a questionnaire to evaluate mathematics teachers’ beliefs about mathematics, teaching, and learning. Eurasia Journal of Mathematics, Science and Technology Education, 20(5), em2435. https://doi.org/10.29333/ejmste/14447
Askew, M., Brown, M., Rhodes, V., Johnson, D., & Wiliam, D. (1997). Effective teachers of numeracy: final report. London, King’s College. https://r.issu.edu.do/QC
Bermejo, V., Ester, P., & Morales, I. (2021). A Constructivist Intervention Program for the Improvement of Mathematical Performance Based on Empiric Developmental Results (PEIM). Frontiers in Psychology, 11. https://doi.org/10.3389/fpsyg.2020.582805
Beswick, K. (2005). The beliefs/practice connection in broadly defined contexts. Mathematics Education Research Journal, 17, 39-68. https://doi.org/10.1007/BF03217415
Beswick, K. (2012). Teachers’ beliefs about school mathematics and mathematicians’ mathematics and their relationship to practice. Educational Studies in Mathematics, 79(1), 127-147. https://doi.org/10.1007/s10649-011-9333-2
Calleja, J. (2022). Changes in mathematics teachers’ self-reported beliefs and practices over the course of a blended continuing professional development programme. Mathematics Education Research Journal, 34(4), 835-861. https://doi.org/10.1007/s13394-021-00366-x
Camero Reinante, Y., Martínez Casanova, L., & Pérez Payrol, V. B. (2016). El desarrollo de la Matemática y su relación con la tecnología y la sociedad. Caso típico. Revista Universidad y sociedad, 8(1), 97-105. https://r.issu.edu.do/Q6
Clark, L. M., DePiper, J. N., Frank, T. J., Nishio, M., Campbell, P. F., Smith, T. M., Griffin, M. J., Rust, A. H., Conant, D. L., & Choi, Y. (2014). Teacher characteristics associated with mathematics teachers’ beliefs and awareness of their students’ mathematical dispositions. Journal for Research in Mathematics Education, 45(2), 246284. https://doi.org/10.5951/jresematheduc.45.2.0246
Corkin, D., Ekmekci, A., & Papakonstantinou, A. (2015). Antecedents of teachers’ educational beliefs about mathematics and mathematical knowledge for teaching among in-service teachers in high poverty urban schools. Australian Journal of Teacher Education, 40(9), 31-62. https://doi.org/10.14221/ajte.2015v40n9.3
Creswell, J. W. (2012). Educational Research: Planning, Conducting and Evaluating Quantitative and Qualitative Research. Pearson.
Dayal, H., & Lingam, G. (2020). Fijian Secondary Mathematics Teachers’ Beliefs About the Nature of Mathematics and Their Self-Reported Teaching Practices. En Leadership, Community Partnerships and Schools in the Pacific Islands, 77-90. Springer Singapore. https://doi.org/10.1007/978-981-15-6483-3_7
Dayal, H., Cowie, B., & Bakalevu, S. (2019). Practicing Secondary Mathematics Teachers? Beliefs about Mathematics. Directions: Journal of Educational Studies, 33(1), 2-18. https://r.issu.edu.do/G1
Ernest, P. (1989). The Knowledge, Beliefs and Attitudes of the Mathematics Teacher: a model. Journal of Education for Teaching, 15(1), 13-33. https://doi.org/10.1080/0260747890150102
Furinghetti, F., & Morselli, F. (2011). Beliefs and beyond: Hows and whys in the teaching of proof. ZDM, 43(4), 587-599. https://doi.org/10.1007/S11858-011-0316-7
Goos, M., Ní Ríordáin, M., Faulkner, F., & Lane, C. (2021). Impact of a national professional development programme for out-of-field teachers of mathematics in Ireland. Irish Educational Studies, 42(3), 401-421. https://doi.org/10.1080/03323315.2021.1964569
Grigutsch, S., Raatz, U., & Torner, G. (1998). Einstellungen gegenuber mathematik bei mathematiklehrern. Journal Fur Mathematik-Didaktik, 19(1), 3-45. https://doi.org/10.1007/BF03338859
Guangbao, F., & Timothy, T. (2021). Investigating the Associations of Constructivist Beliefs and Classroom Climate on Teachers’ Self-Efficacy Among Australian Secondary Mathematics Teachers. Frontiers in Psychology, 12. https://doi.org/10.3389/fpsyg.2021.626271
Hernández Sampieri, R., Fernández Collado, C., & Baptista Lucio, M. (2014). Capítulo 9, Recolección de datos cuantitativos. En R. Hernández Sampieri, Metodología de la investigación, 194-267. https://r.issu.edu.do/pPg
Kardanova, E., Ponomaryova, A., Safuanov, I., & Osin, E. (2014). Comparative Study of secondary school mathematics teachers’ beliefs and practices in Russia, Estonia and Latvia. Вопросы Образования (Voprosy Obrazovaniya), 2, 44-81. https://dx.doi.org/10.17323/1814-9545-2014-2-44-81
Koklu, O., & Phan, P. (2020). Implementation of STEM in Secondary Mathematics Classrooms: Identification of Teachers’ Beliefs. International Journal of Humanities and Applied Social Science, 5(9). https://doi.org/10.33642/ijhass.v5n9p1
Ministerio de Educación Nacional. (1998). Lineamientos curriculares de matemáticas. https://r.issu.edu.do/va
Ministerio de Educación Nacional. (2006). Estándares básicos de competencias en matemáticas. https://r.issu.edu.do/JS
Misfeldt, M., Jankvist, U. T., & Aguilar, M. S. (2016). Teachers’ beliefs about the discipline of mathematics and the use of technology in the classroom. Mathematics Education, 11(2), 395-419. https://doi.org/10.12973/iser.2016.2113a
Muhtarom, M., Juniati, D., Siswono, T. Y. E., & Rahmatika, I. (2018). Teachers’ and students’ beliefs in mathematics at State Senior High School 5 Sema-rang. Jurnal Riset Pendidikan Matematika, 5(1), 64. https://doi.org/10.21831/jrpm.v5i1.18734
National Council of Teachers of Mathematics. (2015). Principles to actions: Ensuring mathematics success for all. Reston: National Council of Teachers of Mathematics.
Pajares, F. (1992). Teachers’ Beliefs and Educational Research: Cleaning Up a Messy Construct. Review of Educational Research, 62(3), 307-332. https://doi.org/10.3102/00346543062003307
Philipp, A. (2007). Mathematics teachers’ beliefs and affect. En F. K. Lester (Ed.), Second Handbook of Research on Mathematics Teaching and Learning, 1, 257-315. Reston: National Council of Teachers of Mathematics.
Presidente de la República de Colombia. (2002, 19 de junio). Decreto 1278 de 2002, por el cual se expide el Estatuto de Profesionalización Docente. Diario Oficial 44.828. https://r.issu.edu.do/EN
Purnomo, Y. W. (2017). The complex relationship between teachers’ mathematics-related beliefs and their practices in mathematics class. New Educational Review, 47(1), 200-210. https://dx.doi.org/10.15804/tner.2017.47.1.16
Raymond, A. M. (1997). Inconsistency between a beginning elementary school teacher’s mathematics beliefs and teaching practice. Journal for research in mathematics education, 28(5), 550-576. https://doi.org/10.2307/749691
Safrudiannur, & Rott, B. (2021). Offering an Approach to Measure Beliefs Quantitatively: Capturing the Influence of Students’ Abilities on Teachers’ Beliefs. International Journal of Science and Mathematics Education, 19(2), 419-441. https://doi.org/10.1007/s10763-020-10063-z
Schoenfeld, A. (1998). Toward a theory of teaching-in-context. Issues in Education, 4(1), 1-94. https://doi.org/10.1016/s1080-9724(99)80076-7
Siswono, T., Kohar, A., Hartono, S., Rosyidi, A., Kurniasari, I., & Karim, K. (2016). Instrumentalist teachers’ beliefs in practicing mathematical problem solving. Universal Journal of Educational Research, 7(12), 2851-2856. https://doi.org/10.13189/ujer.2019.071236
Siswono, T., Kohar, A., Hartono, S., Rosyidi, A., Kurniasari, I., & Karim, K. (2019). Examining teacher mathematics-related beliefs and problem-solving knowledge for teaching: Evidence from Indonesian primary and secondary teachers. International Electronic Journal of Elementary Education, 11(5), 493-506. https://doi.org/10.26822/iejee.2019553346
Skovsmose, O., & Valero, P. (2013). Breaking political neutrality: The critical engagement of mathematics education with democracy. Sociocultural research on mathematics education (pp. 37-55). Routledge.
Swan, M., & Swain, J. (2010). The impact of a professional development programme on the practices and beliefs of numeracy teachers. Journal of Further and Higher Education, 34(2), 165-177. https://doi.org/10.1080/03098771003695445
Šunderlík, J., & Rybanský, Ľ. (2015). Developing and piloting an instrument for measuring upper secondary mathematics teachers beliefs in Nitra Region. Acta Mathematica Nitriensia [Mathematical Journal of Nitra], 1(1), 128-134. https://doi.org/10.17846/amn.2015.1.1.128-134
Thompson, A. G. (1992). Teachers’ beliefs and conceptions: A synthesis of the research. En D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning: A project of the National Council of Teachers of Mathematics (pp. 127-146). Macmillan Publishing Co.
Thurm, D., & Barzel, B. (2020). Effects of a professional development program for teaching mathematics with technology on teachers’ beliefs, self-efficacy and practices. ZDM - Mathematics Education, 52(7), 1411-1422. https://doi.org/10.1007/s11858-020-01158-6
UNESCO. (2015). Informe de resultados TERCE. Tercer Estudio Regional Comparativo y Explicativos. Factores Asociados. Santiago, Chile: Oficina Regional de Educación para América Latina y el Caribe. (OREALC/UNESCO Santiago). https://r.issu.edu.do/l?l=248MoC
Vale, C., Campbell, C., & White, P. (2021). Beliefs and practices of secondary teachers crossing subject boundaries to teach mathematics out-of-field. Mathematics Education Research Journal, 33(3), 589-612. https://doi.org/10.1007/s13394-020-00323-0
Vale, C., Campbell, C., Speldewinde, C., & White, P. (2020). Teaching Across Subject Boundaries in STEM: Continuities in Beliefs about Learning and Teaching. International Journal of Science and Mathematics Education, 18(3), 463-483. https://doi.org/10.1007/s10763-019-09983-2
Vesga-Bravo, G. J., & Angel-Cuervo, Z. M. (2021). Contraste entre la práctica y las creencias epistemológicas sobre las matemáticas, su enseñanza y aprendizaje. Un estudio de casos con docentes de matemáticas en formación. Bolema: Boletim de Educação Matemática, 35(70), 637-663. https://doi.org/10.1590/1980-4415v35n70a05
Vintere, A. (2018). A Constructivist Approach to the Teaching of Mathematics to Boost Competences Needed for Sustainable Development. Rural Sustaina-bility Research, 39(334), 1-7. https://dx.doi.org/10.2478/plua-2018-0001
Wang, T., & Cai, J. (2007). Chinese (Mainland) teachers’ views of effective mathematics teaching and learning. ZDM - International Journal on Mathematics Education, 39(4), 287-300. https://doi.org/10.1007/s11858-007-0030-7
Xenofontos, C. (2018). Greek-Cypriot elementary teachers’ epistemological beliefs about mathematics. Teaching and Teacher Education, 70, 47-57. https://doi.org/10.1016/j.tate.2017.11.007
Xie, S., & Cai, J. (2021). Teachers’ Beliefs about Mathematics, Learning, Teaching, Students, and Teachers: Perspectives from Chinese High School In-Service Mathematics Teachers. International Journal of Science and Mathematics Education, 19(4), 747-769. https://doi.org/10.1007/s10763-020-10074-w
Contribución de autores
Conceptualización: A.Z., B.J.; metodología: A.Z., B.J.; software: A.Z., B.J., B.A.; validación: A.Z.; análisis formal: A.Z.; investigación: A.Z., B.J., B.A.; recursos: A.Z.; curaduría de datos: A.Z.; escritura (borrador original): A.Z., B.J.; escritura (revisión y edición): A.Z., B.J., B.A.; visualización: A.Z.; supervisión: A.Z., B.J., B.A.; administración del proyecto: A.Z.